并查集小结

发表于 | 分类于 | |

今天刷LeetCode 547.Friend Circles 时发现，其就是一道典型的并查集。但是还是不能靠本科学的数据结构知识写出完整的代码，所以就趁机将并查集小结一下，主要参考资料是普林斯顿大学的《Algorithm 4th》。

并查集，顾名思义，就是通过边并边查，把有直接或间接联系的元素都划分到同一个集合里。主要有以下两个步骤：

  1. 查（Find）：给定联系p,q，查一查p,q是否已经在同一个集合了。
  2. 并（Union）：如果p,q分别在不同的集合里，就合并。

关于查和并这两个的操作主要由三种思路。

快查(Quick-find)：

​ 通过维护一个id数组，保存着每个元素所在集合的代表，这样查的时候只要查一查代表是谁就知道两个元素所在集合是不是同一个集合了。如果同在某个集合，则有：

id[p]==id[q]

​ 如果不在的话进行合并的时候，就需要把其中某个集合里的所有元素的id值改为另一个集合的代表。如下图所示：

​ 快查慢并

Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public QuickFindUF(int n)
{
  count = n;
  vector<int> id;
  id.resize(n);
  for(int i = 0 ; i < n ; i++)
  {
    id[i] = i;
  }
}

pubinc int find(int p)
{
  return id[p];
}

public void Union(int p,int q)
{
  int pID = id[p];
  int qID = id[q];
  
  if(pID==qID)
    return;
  
  for(int i = 0 ; i < n; i++)
  {
    if(id[i]==pID) id[i] = qID;
  }
  count --;
}

​ 查的复杂度：O(1)

​ 并的复杂度：O(n)

快并(Quick-Union)：

​ 鉴于快查方法中并的操作复杂度为O(n)，我们就要想方设法降低复杂度。

​ 这次我们还是维护一个id数组，但是这个数组保存已经不再是集合代表了，而是它的父节点（parent node）。相当于维护一个单向列表（除了根节点要自己指向自己）。

​ 这样合并的时候只需要将某个集合的根节点指向另一个集合的根节点即可。

​ 示意图如下：

​

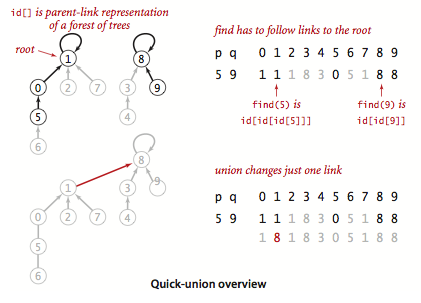
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public QuickUnionUF(int n)
{
  count = n;
  vector<int> id;
  id.resize(n);
  for(int i = 0 ; i < n ; i++)
  {
    id[i] = i;
  }
}

pubinc int find(int p)
{
  while(p!=id[p])
    p = id[p];
  return p;
}

public void Union(int p,int q)
{
  int pRoot = find(p);
  int qRoot = find(q);
  
  if(pRoot==qRoot)
    return;
  
  id[pRoot] = qRoot;
  
  count --;
}

​ 查的复杂度O（logn）

​ 并的复杂度O（1）

平衡地并(Weighted quick-union)：

​ 上述的做法虽然在一定程度上优化了复杂度。但是对于某些情况，对导致搜索的深度达到O(n)，复杂度还是会比较差。所以要避免这种情况，就还需要继续对上一种做法继续优化。

​ 快并做法在合并两个集合时某个集合的根节点指向另一个集合的根节点这个完全是随机的。我们可以在这儿优化一下，让小的集合（深度较浅）的指向大的集合的根节点（深度较深），经过这样的优化，合并后的树的深度并没有增加，还是等于原来深度较深的那颗数的深度。

​ 所以，我们只需要多申请一个数组sz[i]，用来记录以i为根的树已经包含了多少个节点了。然后在合并的时候做下判断后再进行合并即可。

​ 示意图如下：

​

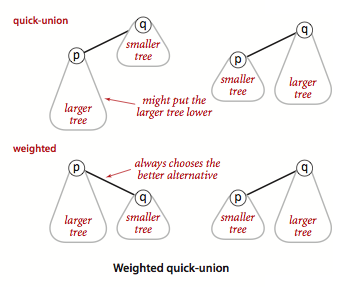
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public QWeightQuickUnionUF(int n)
{
  count = n;
  vector<int> id;
  vector<int> sz;
  id.resize(n);
  sz.resize(n);
  for(int i = 0 ; i < n ; i++)
  {
    id[i] = i;
    sz[i] = 1;
  }
}

pubinc int find(int p)
{
  while(p!=id[p])
    p = id[p];
  return p;
}

public void Union(int p,int q)
{
  int pRoot = find(p);
  int qRoot = find(q);
  
  if(pRoot==qRoot)
    return;
  
  if(sz[pRoot] < sz[qRoot])
  {
    id[pRoot] = qRoot;
    sz[qRoot] += sz[pRoot];
  }
  else
  {
    id[qRoot] = pRoot;
    sz[pRoot] += sz[qRoot];
  }
  
  count --;
}

看完之后竟然能把LeetCode547的代码一遍无误地敲出来了。看来是看国外的书还是能够深入浅出，默默地思想根植在脑海中。Excited~!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//
// Created by chaopengz on 2017/11/6.
//
#include "head.h"

class Solution {
public:
    int findCircleNum(vector<vector<int>> &M)
    {
        if (!M.size())
            return 0;
        int n = M[0].size();
        count = n;

        id.resize(n);
        sz.resize(n);

        for (int i = 0; i < n; ++i)
        {
            id[i] = i;
            sz[i] = 1;
        }


        for (int i = 0; i < n - 1; ++i)
        {
            for (int j = i + 1; j < n; ++j)
            {
                if (M[i][j])
                {
                    Union(i, j);
                }
            }
        }
        return count;
    }

    int Find(int i)
    {
        while (i != id[i])
            i = id[i];
        return i;
    }

    void Union(int i, int j)
    {
        int p = Find(i);
        int q = Find(j);
        if (p == q)
            return;
        if (sz[p] < sz[q])
        {
            id[p] = q;
            sz[q] += sz[p];
        } else
        {
            id[q] = p;
            sz[p] += sz[q];
        }
        count--;
    }

    vector<int> id;
    vector<int> sz;
    int count;
};

Reference：

  1. https://algs4.cs.princeton.edu/15uf/