337. House Robber III

发表于 | 分类于 | |

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Determine the maximum amount of money the thief can rob tonight without alerting the police.

Example 1:

1
2
3
4
5
6
7
>      3
>     / \
>    2   3
>     \   \ 
>      3   1
>
>

>

Maximum amount of money the thief can rob =

3+ 3 + 1 = 7

Example 2:

1
2
3
4
5
6
7
>      3
>     / \
>    4   5
>   / \   \ 
>  1   3   1
>
>

>

Maximum amount of money the thief can rob =

4 + 5 = 9

Credits:
Special thanks to @dietpepsi for adding this problem and creating all test cases.

​ 题意：一颗二叉树中，不同在一条边的节点中，和最大的是多少？

​ 因为刚做二叉树的总结，知道了二叉树大概的处理思路：空值—>根节点—>左右子树。所以这道题最主要也还是大体按照这个思路进行求解。

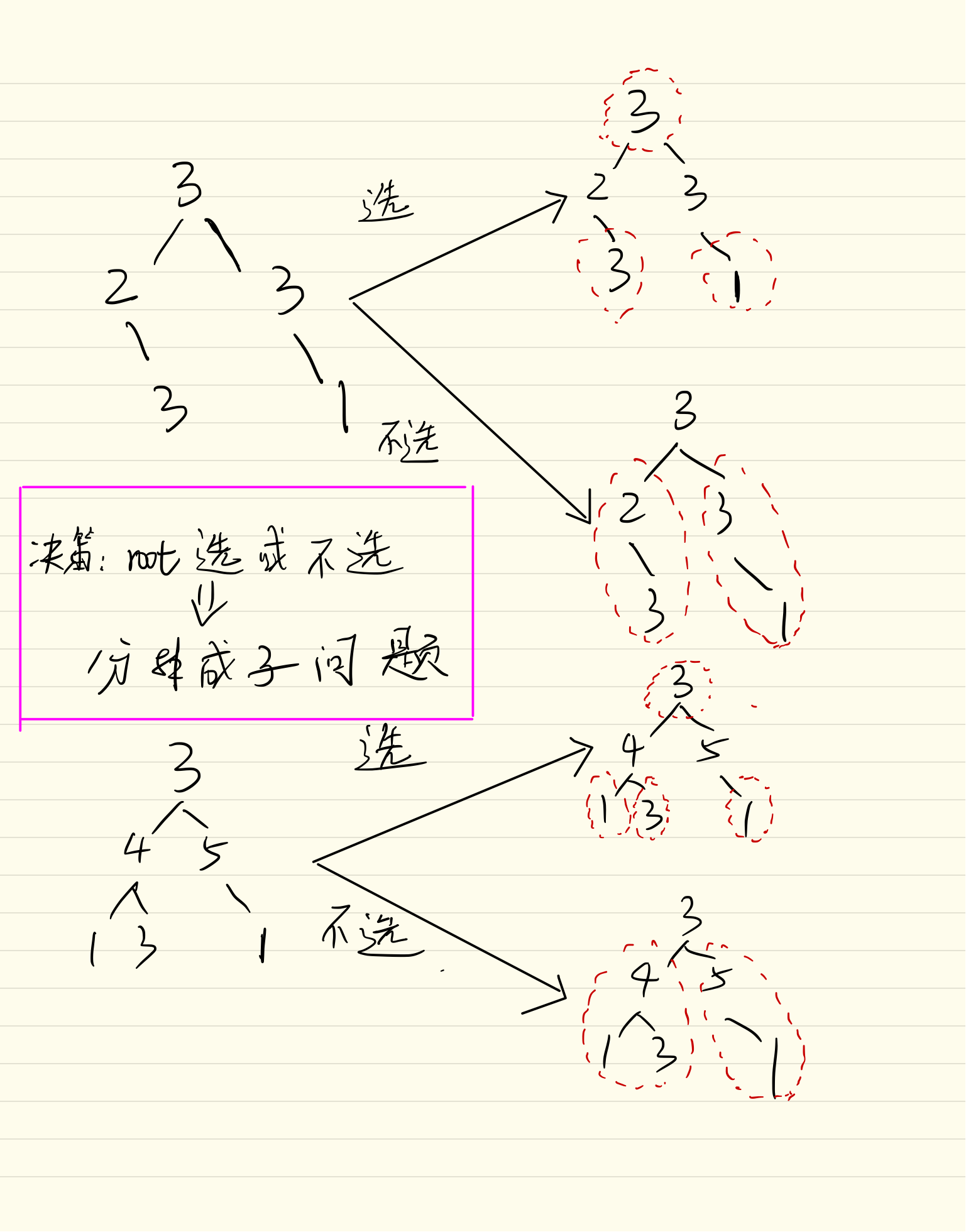
​ 对于每一个根节点，无非就两种选择：选或者不选。

  1. 根节点选了，那么只能根节点的左右孩子都不能再选了，只能选出以孙子为根节点时（子问题）和的最大值之和

  2. 根节点如果没选，那么此时和最大就是分别以左右孩子为根节点时（子问题）的和的最大值之和。

​ 一开始出错的地方在于：因为越了一层进行处理，忘了要对二级指针进行是否为空指针进行判断。

具体代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//
// Created by chaopengz on 2017/11/15.
//

#include "head.h"

class Solution {
public:
    int rob(TreeNode *root)
    {
        if (!root)
            return 0;

        if (!root->left && !root->right)//leaf node
            return root->val;

        if (root->left && root->right)
            return max(rob(root->left) + rob(root->right),
                       root->val + rob(root->left->left) + rob(root->left->right) + rob(root->right->left) +
                       rob(root->right->right));
        if (root->left)//越了一层，需要用到二级指针，所以进行非空判断
            return max(rob(root->left) + rob(root->right),
                       root->val + rob(root->left->left) + rob(root->left->right));
        else
            return max(rob(root->left) + rob(root->right),
                       root->val + rob(root->right->left) + rob(root->right->right));
    }

};