494. Target Sum

发表于 | 分类于 | |

You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
> Input: nums is [1, 1, 1, 1, 1], S is 3. 
> Output: 5
> Explanation: 
>
> -1+1+1+1+1 = 3
> +1-1+1+1+1 = 3
> +1+1-1+1+1 = 3
> +1+1+1-1+1 = 3
> +1+1+1+1-1 = 3
>
> There are 5 ways to assign symbols to make the sum of nums be target 3.
>
>

>

Note:

  1. The length of the given array is positive and will not exceed 20.
  2. The sum of elements in the given array will not exceed 1000.
  3. Your output answer is guaranteed to be fitted in a 32-bit integer.

​ 题意：给出一个数组，每个数前面可以添加正负号的其中一种，凑成一个表达式，求表达式之和刚好等于target有多少种可能性。

​ 一开始采用的是递归的写法，类似于二叉树的打印路径的思想。当走到最后一个数字是，判断此时的和是否刚好为target，如果是，则ans++。

​ 这种思想还犯了一个致命的错误：全局变量保存在堆里面，没有被销毁，临时变量保存在栈里面，会被销毁。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//
// Created by chaopengz on 2017/11/16.
//
#include "head.h"

class Solution {
public:
    int findTargetSumWays(vector<int> &nums, int S)
    {
        findSumRecur(nums, 0, S);

        return ans;

    }

    void findSumRecur(vector<int> nums, int i, int target)
    {
        if (i == nums.size())
        {
            if (target == 0)
                ans++;
            return;
        } else
        {
            int subSum1 = target - nums[i];
            int subSum2 = target + nums[i];
            cout << subSum1 << " " << subSum2 << endl;
            j = ++i;//致命错误，此时j是全局变量，不会被销毁
            cout << "j=" << j << endl;
            findSumRecur(nums, j, subSum1);
            findSumRecur(nums, j, subSum2);
        }

    }

    int ans = 0;
    int j;
};

递归的正确写法但是超时了，显然递归的时间开销太大了。得改用其他思路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//
// Created by chaopengz on 2017/11/16.
//
#include "head.h"

class Solution {
public:
    int findTargetSumWays(vector<int> &nums, int S)
    {
        findSumRecur(nums, 0, S);

        return ans;

    }

    void findSumRecur(vector<int> nums, int i, int target)
    {
        if (i == nums.size())
        {
            if (target == 0)
                ans++;
            return;
        } else
        {
            int subSum1 = target - nums[i];
            int subSum2 = target + nums[i];
            int j = ++i;//正确地写法，会在每一个递归栈里有一个临时变量
            findSumRecur(nums, j, subSum1);
            findSumRecur(nums, j, subSum2);
        }

    }

    int ans = 0;

};

​ 后来仔细一想，这个问题其实就是背包的变种，在背包问题中，状态转移的条件是：选或不选，在这个问题则是，加还是减。

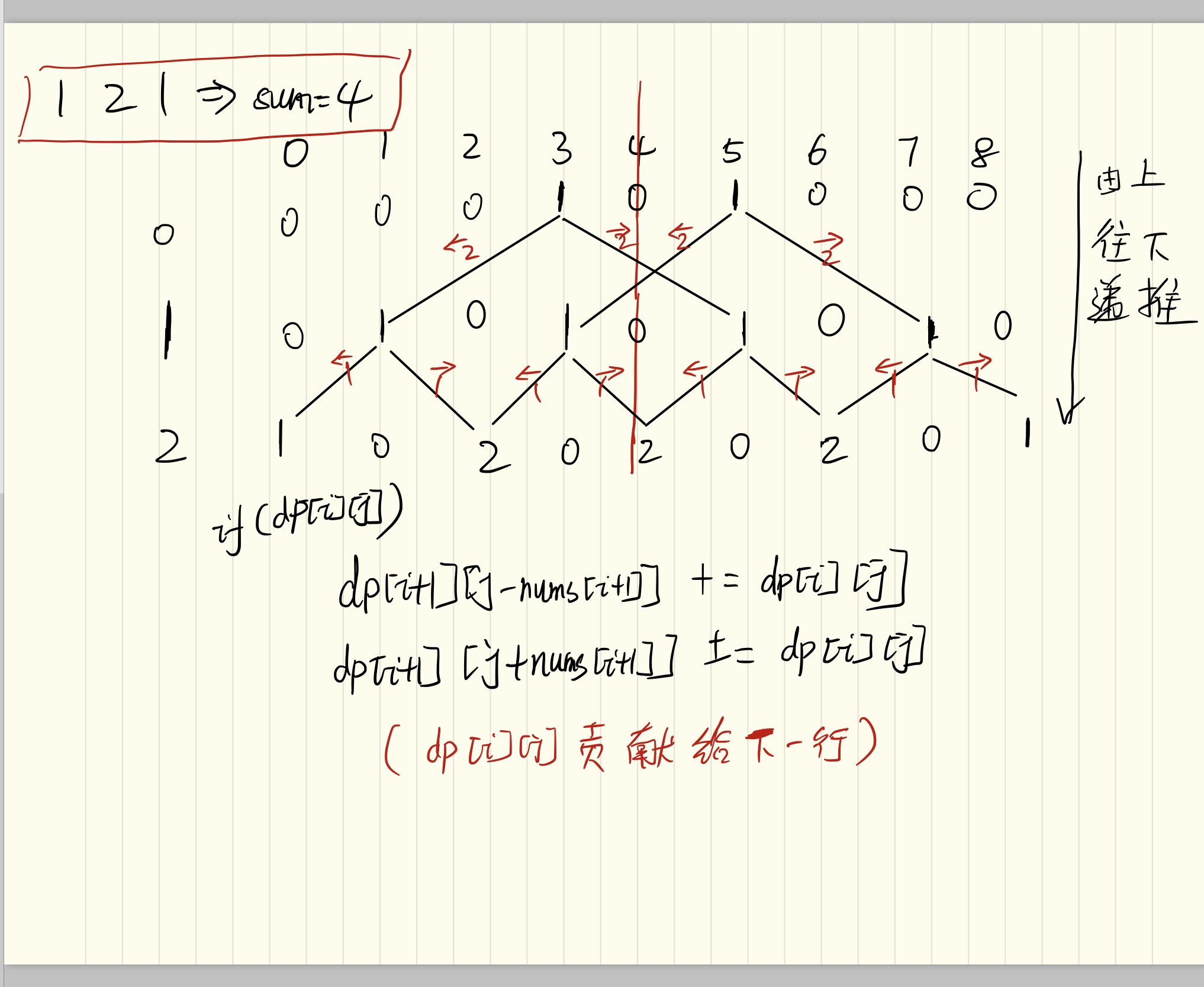
定义状态：dp[i][j]: 数组前i个数字组成的表达式之和为j的可能性种数。

这样状态转移方程为： dp[i][j] = dp[i-1][ j+nums[i] ] + dp[i-1][ j-nums[i] ]

虽然思路是对的，但是实现起来还是有很多需要注意的细节，比如刚实现dp在本地是对的，但是提交到远程就错了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//
// Created by chaopengz on 2017/11/16.
//
#include "head.h"

class Solution {
public:
    int findTargetSumWays(vector<int> &nums, int S)
    {
        int N = 20000;
        vector<vector<int>> dp;
        dp.resize(20, vector<int>(N));

        for (int j = -N/2; j < N/2; ++j)
        {
            if (!nums[0])//第一个为0,则dp[0][0]有两个解，正0和负0
                dp[0][0] = 2;
            else if (j == nums[0] || j == -nums[0])
                dp[0][j] = 1;
            else
                dp[0][j] = 0;
        }

        for (int i = 1; i < nums.size(); ++i)
        {
            for (int j = 0; j < N; ++j)
            {
                dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j + nums[i]];
            }
        }
        return dp[nums.size() - 1][S];
    }
};

​ 错的主要原因就是dp的第二维：j - nums[i]，有可能是小于0的数。这样递推起来肯定就有问题了。所以咋办呢？

​ 其实上述代码的主要思路是这样的：第i行第j列是由第i-1行的两个具体列（j-nums[i],j+nums[i]）来决定的，这样就在找j-nums[i]列时可能就找不到了。

​ 不妨换个角度思考，既然第i行由第i-1行来决定，那么是不是也意味着，第i行可以决定第i+1行的数据呢？也就是说，对第i行中每个不为0的数，都会被加到下一行(i+1)的j+nums[i+1] 和j-nums[i+1]这两列中去。因为题意说sum之和不会超过1000，并且我们把列数都进行了平移（第二维度的坐标从-sum -> +sum），所以就能保证j-nums[i+1]一定不会小于0啦~

​ 具体可以看图示：

最后终于AC了的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
//
// Created by chaopengz on 2017/11/16.
//
#include "head.h"

class Solution {
public:
    int findTargetSumWays(vector<int> &nums, int S)
    {
        int sum = 0;
        for(auto i:nums)
            sum += i;
        int cols = 2*sum+1;
        if (S > sum || S< -sum)
            return 0;

        int dp[20][4005];
        memset(dp, 0, sizeof(dp));

        for (int j = 0; j < cols; ++j)
        {
            if (!nums[0])//第一个为0,则dp[0][sum]有两个解，正0和负0
                dp[0][sum] = 2;
            else if (j == nums[0] + sum || j == -nums[0] + sum)
                dp[0][j] = 1;
            else
                dp[0][j] = 0;
        }

        for (int i = 0; i < nums.size()-1; ++i)
        {
            for (int j = 0; j < cols; ++j)
            {
                //dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j + nums[i]];
                if(dp[i][j])
                {
                    dp[i+1][j-nums[i+1]] += dp[i][j];
                    dp[i+1][j+nums[i+1]] += dp[i][j];
                }
            }
        }

        return dp[nums.size() - 1][sum+S];
    }
};