279. Perfect Squares

发表于 | 分类于 | |

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.

For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.

题意：给出一个数n，判断它最少可以由多少个完全平方数相加而成。

​ 一开始拿到这道题还在那里把1-16的数字都写出来了，想看出什么规律。结果还是太Naive了，比六合彩更没规律。0-0

​ 然后想用贪心的想法：每次都从完全平方数里面挑出一个最大的（假设为nums[i]）并且比n小的，接着再从完全平方数里面挑出最大的并且比n-nums[i]的，…，依次递推。

​ 但是很快就知道贪心的不行，看样例给的12就知道了，12 = 4+4+4 才是最优，按照贪心应该是12=9+1+1+1，得由四个数才相加才能等于12。

​ 看了下Discuss才发现还是dp的问题，看来对dp的理解还是不够深刻，想了那么久都没看出可以用dp来解决这道题。

​ 理解了之后，发现这道题跟刚刚做的最长上升子序列300. Longest Increasing Subsequence 其实异曲同工啊！

​ 定义dp[i]为:=i 由完全平方数组合起来和等于i的最小个数。

那么i可以由之前的状态怎么推导出来呢？

​ 不就是对于所有满足条件的j，dp[i] = dp[i-jj] + 1; 其中 1<= j\j < i;

​ 然后维护dp[i]最小值dp[i] = min(dp[i], dp[i - j * j] + 1)就好了吗？0-0

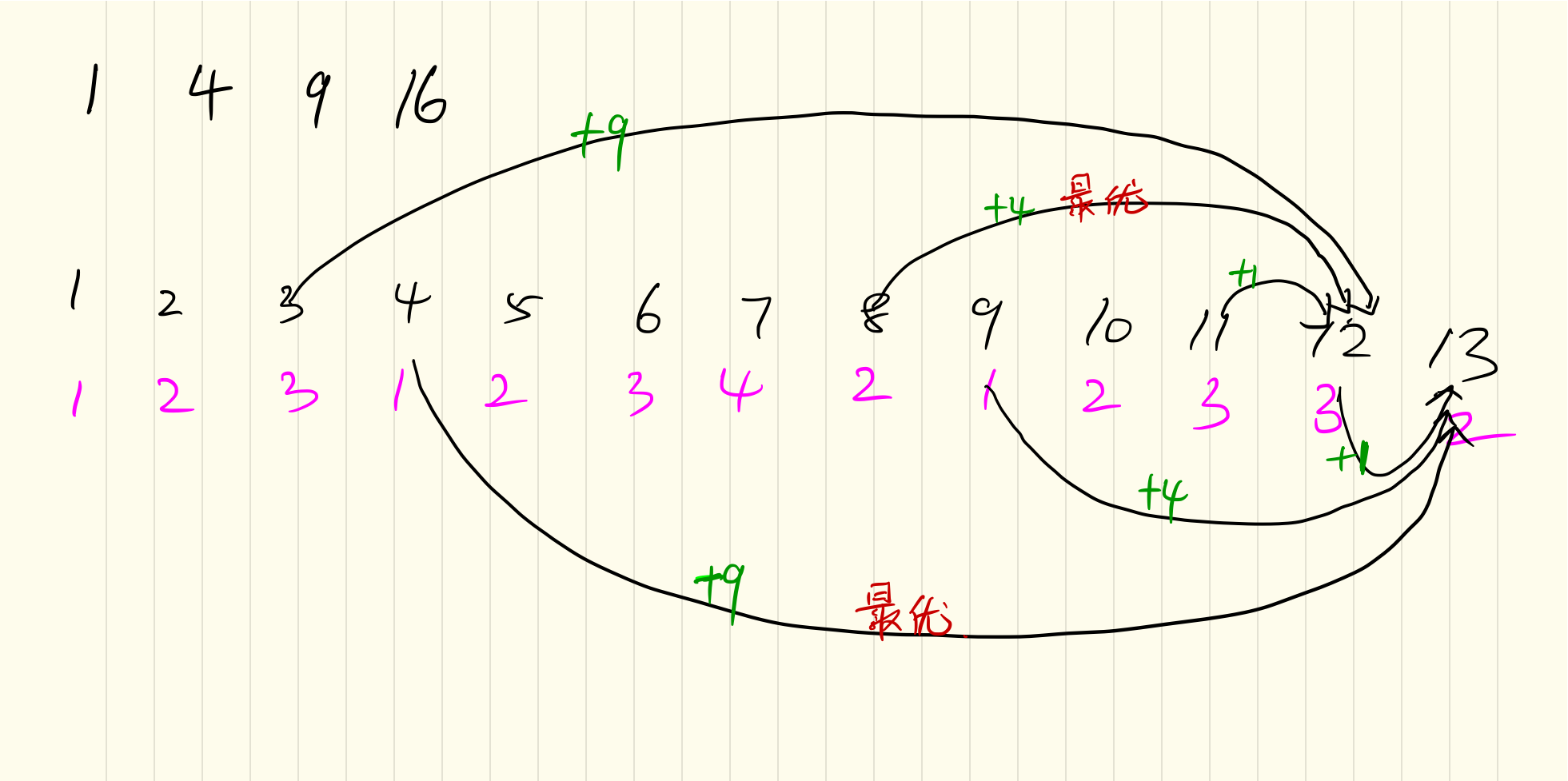
​ 以样例给的12和13为例：

​

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//
// Created by chaopengz on 2017/12/3.
//

#include "head.h"

class Solution {
public:
    int numSquares(int n)
    {
        vector<int> dp(n + 1, INT32_MAX);
        dp[0] = 0;
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 1; j * j <= i; ++j)
            {
                dp[i] = min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }
};