10. Regular Expression Matching

发表于 | 分类于 | |

Implement regular expression matching with support for '.' and '*'.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
> '.' Matches any single character.
> '*' Matches zero or more of the preceding element.
>
> The matching should cover the entire input string (not partial).
>
> The function prototype should be:
> bool isMatch(const char *s, const char *p)
>
> Some examples:
> isMatch("aa","a") → false
> isMatch("aa","aa") → true
> isMatch("aaa","aa") → false
> isMatch("aa", "a*") → true
> isMatch("aa", ".*") → true
> isMatch("ab", ".*") → true
> isMatch("aab", "c*a*b") → true
>

​ 题意：正则匹配，判断p是否匹配s。其中’.’匹配任意单个字符，’*’匹配0个或多个的前一字符。

​ 其实前两个月就刷了这道题，当时虽然也看了题解但是并不能很好理解，甚至看不懂题目的匹配原则。正值昨天浩博来问，发现大体能看懂，就昨晚再重新推导并重写了下代码，AC了。

​ 首先定义状态：

1
dp[i][j] := s串的前i个字符和p串的前j个字符是否能匹配

​ 先初始化dp表，处理当s为空串的情况。

1
2
3
4
5
6
7
8
9
dp[0][0] = true;//都为空是匹配的
     dp[0][1] = false;//s为空，那么p只有一个字符的话是无论如何不能匹配的
     for (int j = 2; j <= n; ++j)//s为空
     {
         if (p[j - 1] == '*')//a*只能出现0次，匹配空串，因为s为空
             dp[0][j] = dp[0][j - 2];
         else//p[j]为.或*
             dp[0][j] = false;
     }

​ 接下来就是推导状态转移了！状态转移的推导主要是根据模式串（p）的最后一个字符（p[j-1]）来决定的。这里我们先看一下这个比较烦人的‘*’号。

1
‘*’代表前一字符可以重复0次或者多次（>=1）。

​ 怎么处理好重复多次应该是这道题最难的地方，根据Discuss里的大佬的提示，可以做如下的处理：

  • 假设‘*’的前一个字符为a,即‘a*’

  1. 重复0次

    最好处理了，只需要判断p串里a符号前的子串能否匹配s串 => dp[i][j] = dp[i][j-2]

  2. 重复多次

    用了一个技巧，把模式串变成了a*a，这样只需要判断：

    1. s串的最后一个字符是否和a相等
    2. 判断dp[i-1][j]是否为true(即，s[0,1,2,3,…,i-2]是否与p[0,1,2,…,j-1] 匹配)

下面用s = “aa” 以及 p=”a*“ 推算一下“*”是怎么匹配两次的。

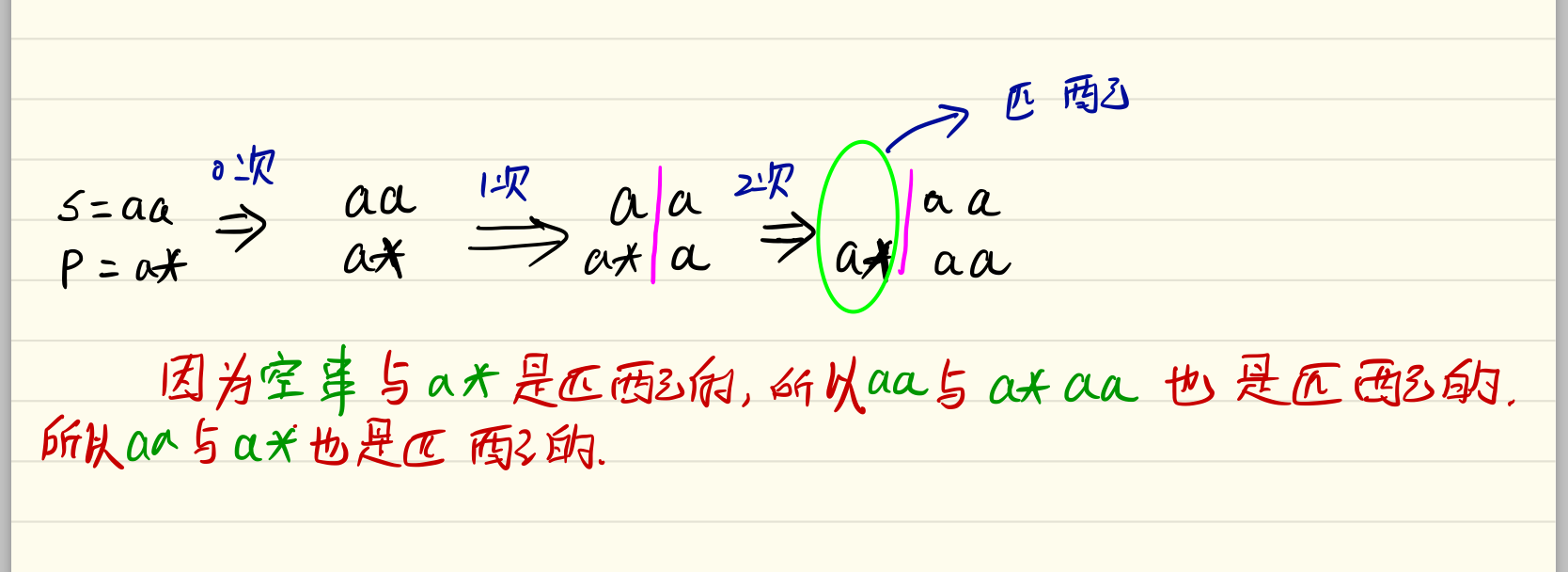
搞明白“*”的多次匹配之后，接下来就进入正式推导了，dp[i][j]的取值主要看p串的最后一个字符（即p[j-1]）。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

//
// Created by chaopengz on 2017/9/25.
//
#include "head.h"

class Solution {
public:
    bool isMatch(string s, string p)
    {
        int m = s.size(), n = p.size();
        vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false));
        dp[0][0] = true;
        dp[0][1] = false;//s为空，那么p只有一个字符的话是无论如何不能匹配的
        for (int j = 2; j <= n; ++j)//s为空
        {
            if (p[j - 1] == '*')//a*只能出现0次，因为s为空
                dp[0][j] = dp[0][j - 2];
            else//p[j]为.或*
                dp[0][j] = false;
        }
        for (int i = 1; i <= m; ++i)
        {
            for (int j = 1; j <= n; ++j)
            {
                if (p[j - 1] == '*')//x*出现0次或者多次
                {
                    if (p[j - 2] == '.')
                    {
                        dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
                    } else
                    {
                        dp[i][j] = dp[i][j - 2] || (s[i - 1] == p[j - 2] && dp[i - 1][j]);
                    }
                } else if (p[j - 1] == '.')
                {
                    dp[i][j] = dp[i - 1][j - 1];
                } else
                {
                    dp[i][j] = dp[i - 1][j - 1] && (s[i - 1] == p[j - 1]);
                }
            }
        }
        return dp[m][n];
    }
};