cs231n

1.Image Classification

slides：Image Classification pipeline

1. L1 与 L2（2范数，欧氏距离）距离

   

2. 交叉验证

   把数据集分成n等份，分别把每一份作为验证集（寻找最优超参数），最后将结果平均。

linear classification notes

1. SVM Loss

$$L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)$$ $$s_{y_i} 比s_j 大至少\Delta，则该项Loss为0\\ s_{y_i} - s_j > \Delta \Rightarrow s_{y_i} - s_j - \Delta > 0 \Rightarrow s_j - s_{y_i} + \Delta < 0$$

Example:

s=[13,−7,11], first class is the true class (i.e. yi=0)

$$L_i = \max(0, -7 - 13 + 10) + \max(0, 11 - 13 + 10)$$

We get zero loss for this pair because the correct class score (13) was greater than the incorrect class score (-7) by at least the margin 10

1. 正则 Regularization

   ​ Prevent the model from doing too well on training data：防止过拟合。

   ​ 按照上述的SVM Loss公式，满足Loss为0的W有多个，最简单地，如果W0满足，那么 $W_0$ 满足，那么 $\lambda W_0$ 也将满足Loss为0。比如用$W_0$ 算出来的距离是15，那么用$2W_0$ 算出来的就是30，依旧大于margin,所以Loss为0.

   ​ 所以，为了不让所有 $\lambda W0$ 都满足Loss为0，可以引入一个正则项，比较常使用的L2正则：$R(W) = \sum_k\sum_l W{k,l}^2$ ，即把W矩阵的各个数字平方都加起来也作为Loss的一部分，这样可以确保W的唯一性。所以加上正则后的SVM Loss应该为：$L = \underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss} + \underbrace{ \lambda R(W) }_\text{regularization loss} \\\\$

   ​ 展开后为:

   ​ $L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l}^2$

2. Softmax Loss

   ​ SVM 和 Softmax是两大常见的分类器。

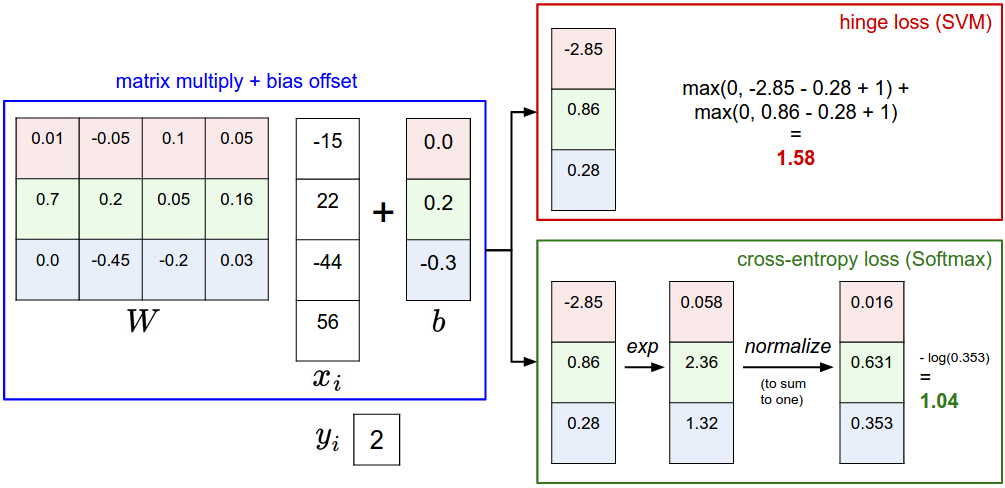
   1. SVM: $f(x_i,W)$ 的输出是未经校准且可能难以解释，Use max-margin loss

   2. Softmax：直观输出（归一化类概率）并且还具有概率解释, Use cross-entropy loss

      $Li = -\log\left(\frac{e^{f{yi}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f{y_i} + \log\sum_j e^{f_j}$

   ​ SVM计算的trick，加一个C参数防止e指数后爆炸：

​ $\frac{e^{f{y_i}}}{\sum_j e^{f_j}} = \frac{Ce^{f{yi}}}{C\sum_j e^{f_j}} = \frac{e^{f{y_i} + \log C}}{\sum_j e^{f_j + \log C}}$

​ 关于C的选择：$\log C = -\max_j f_j$, 使得 加了$C$ 的$f$ 的最大值是0。

​ SVM vs. Softmax:

---

2.Loss Functions and Optimization

slides：Loss Functions and Optimization

Softmax Classifier

1. 如果分类器出来的分数大家都差不多相等，那么Softmax的Loss为 $logC$，C是类别数目。

Optimization

1. 在多个维度中，梯度是沿每个维度的（偏导数）的向量

optimization notes

1. Mini-batch gradient descent 批量梯度下降

   没必要每张图片计算一个梯度，而是一批图片计算Loss得到一个梯度进行下降。

   # Vanilla Minibatch Gradient Descent
   
   while True:
     data_batch = sample_training_data(data, 256) # sample 256 examples
     weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
     weights += - step_size * weights_grad # perform parameter update

2. batch的大小一般是2的整数次幂，因为矢量化操作实现在输入大小为2的情况下工作得更快。

---

3.Introduction to Neural Networks

slides: Backpropagation and Neural Networks

Backpropagation 反向传播

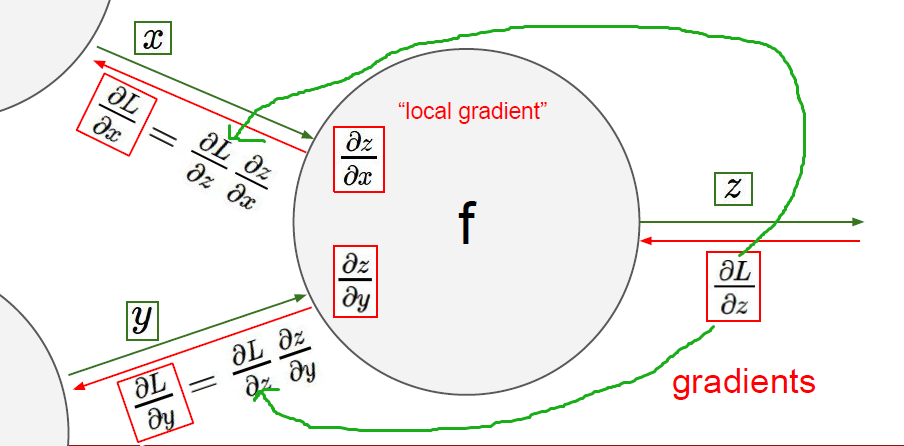
1. 简单的图示

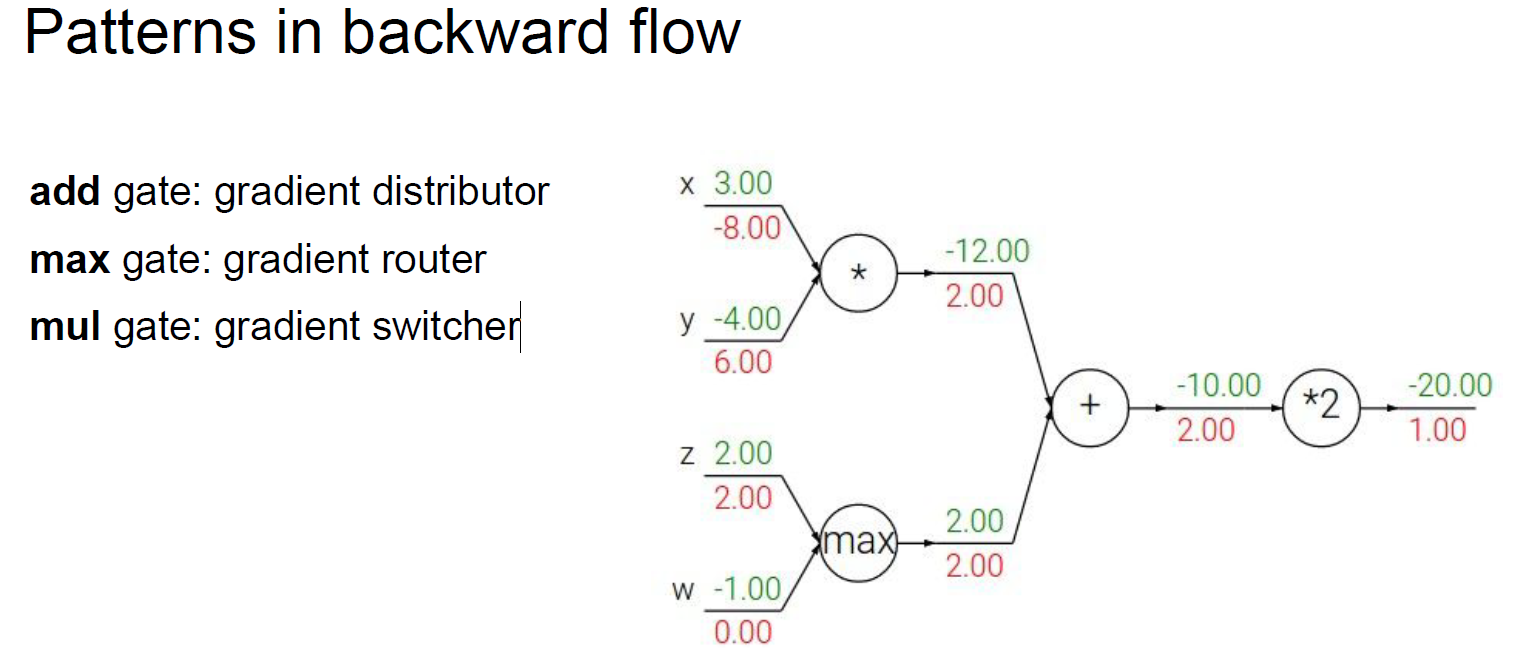
1. 梯度回传模式

   1. 加法：梯度都分给两个输入

   2. max: 梯度路由给最大值

   3. 乘法：把两个input梯度交换

      

2. 矩阵运算的梯度回传

   

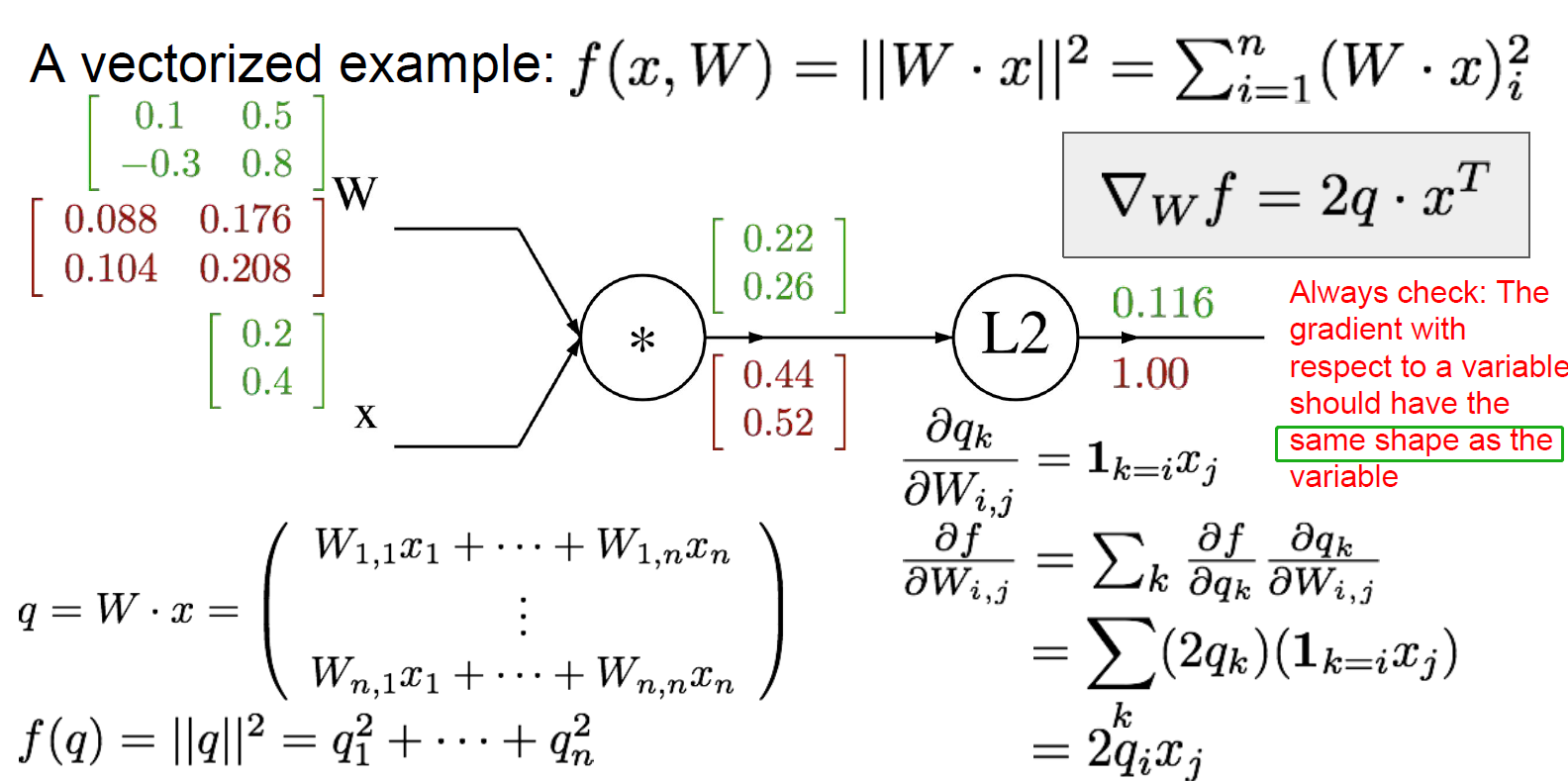
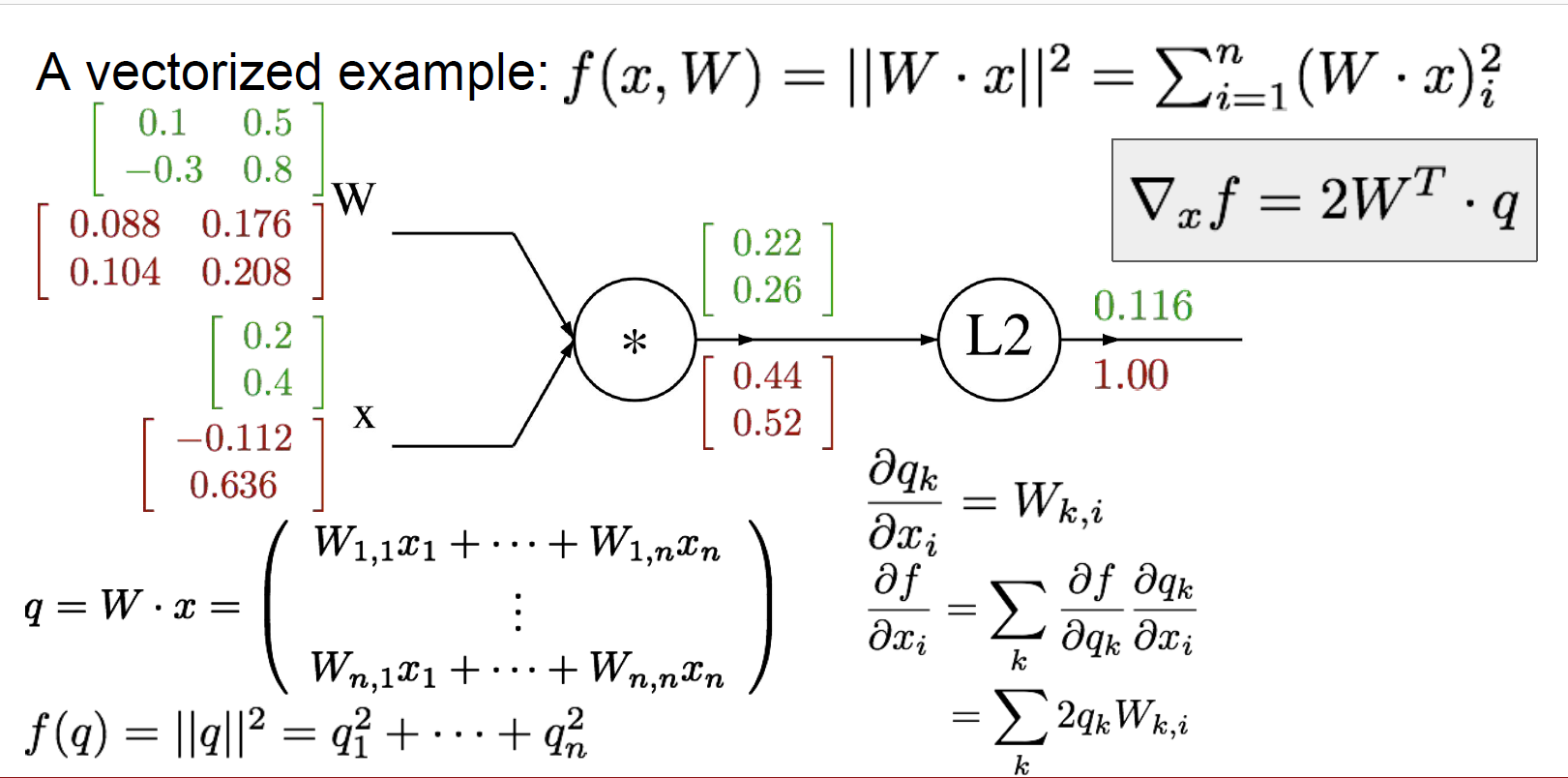
Neural Networks

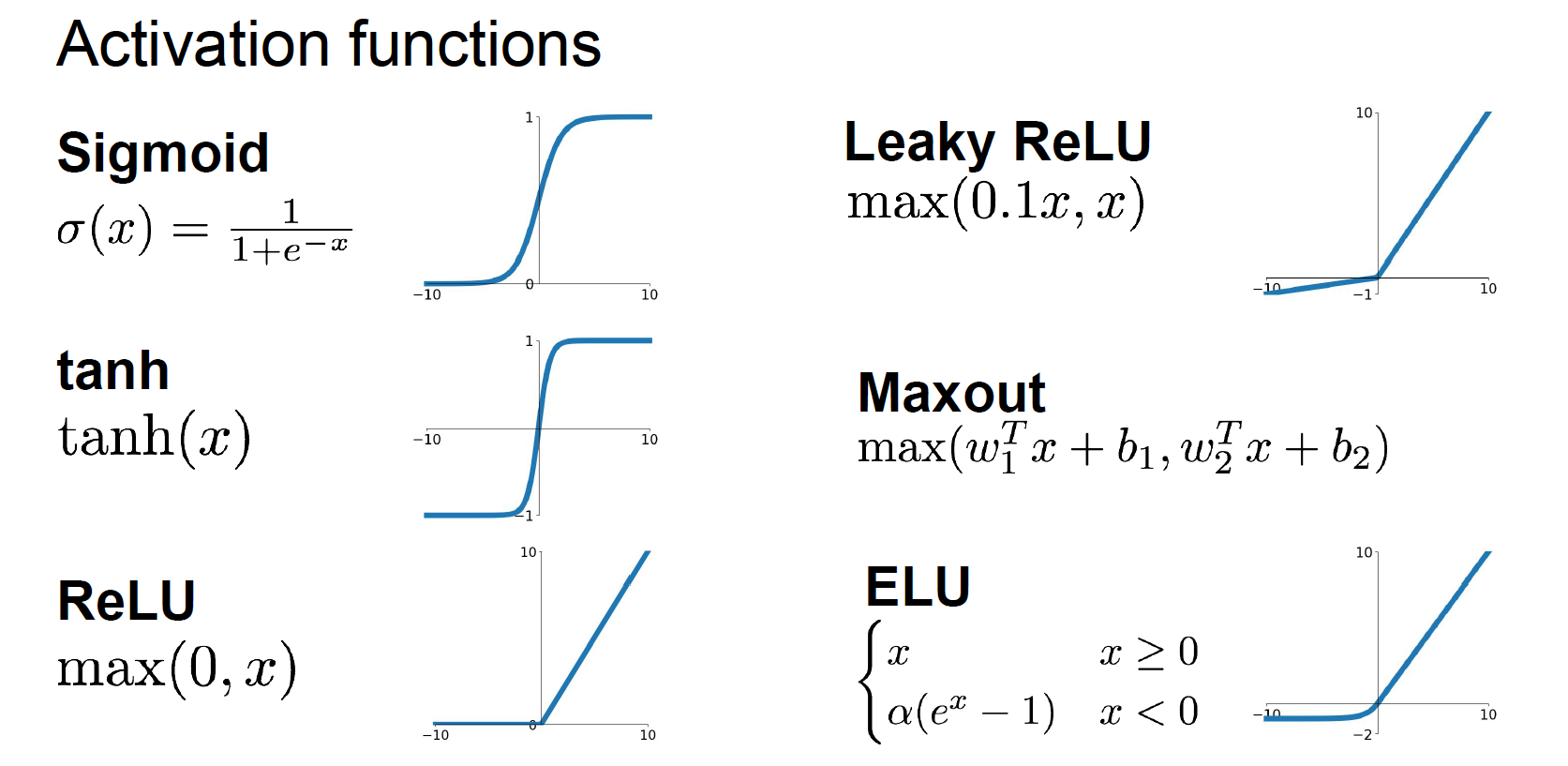
1. 激活函数

   Sigmoid,tanh,ReLU,Leaky ReLU,Maxout,ELU

   

backprop notes

1. Problem statement

   We are given some function $f(x)$ where $x$ is a vector of inputs and we are interested in computing the gradient of $f$ at $x$ (i.e. $\nabla f(x)$).

2. sigmoid 导数

   $$\sigma(x) = \frac{1}{1+e^{-x}} \\\\ \rightarrow \hspace{0.3in} \frac{d\sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2} = \left( \frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) \left( \frac{1}{1+e^{-x}} \right) = \left( 1 - \sigma(x) \right) \sigma(x)$$

---

4.Backpropagation

slides: Backpropagation and Gradients

---

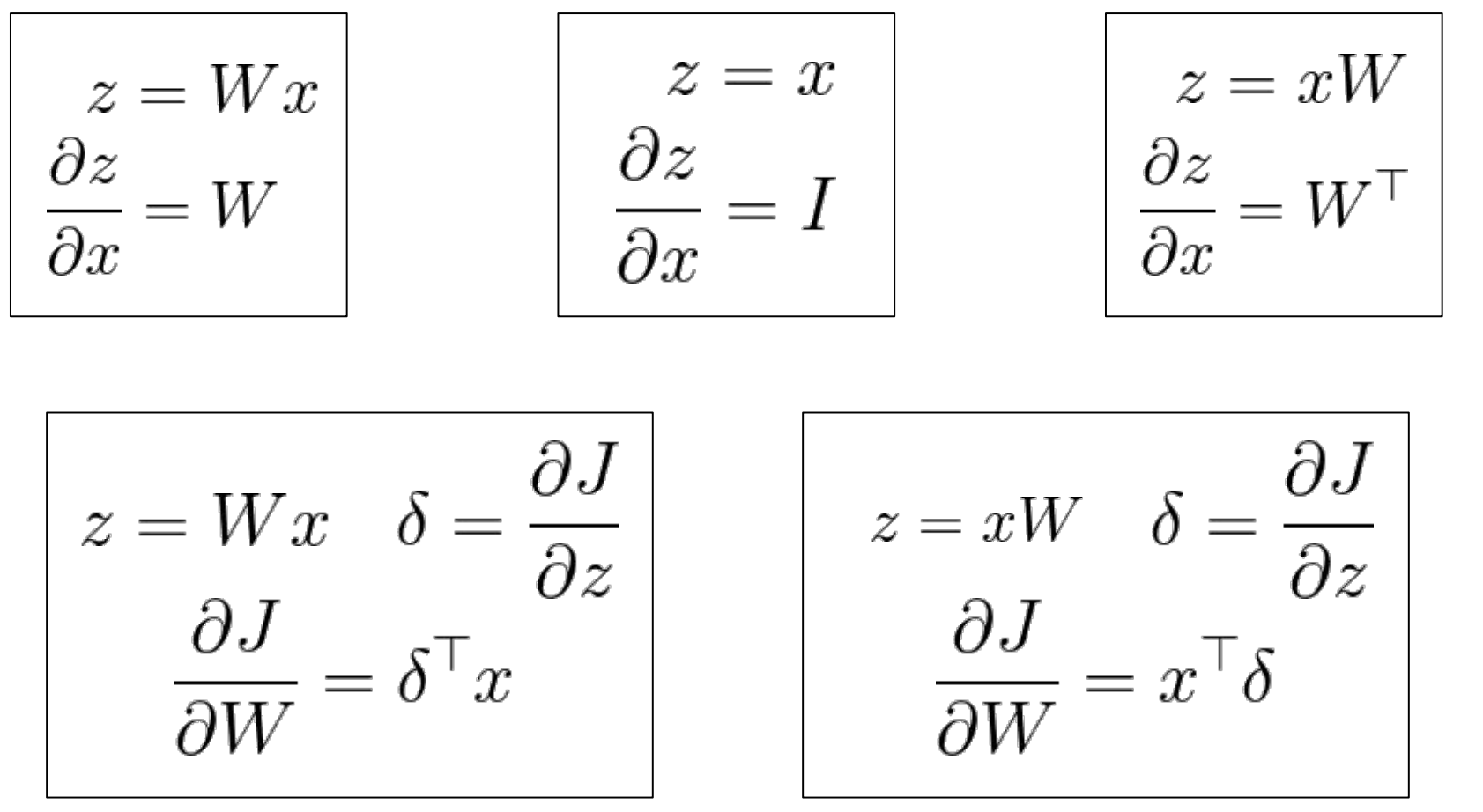
5.Convolutional Neural Networks

slides:Convolutional Neural Networks

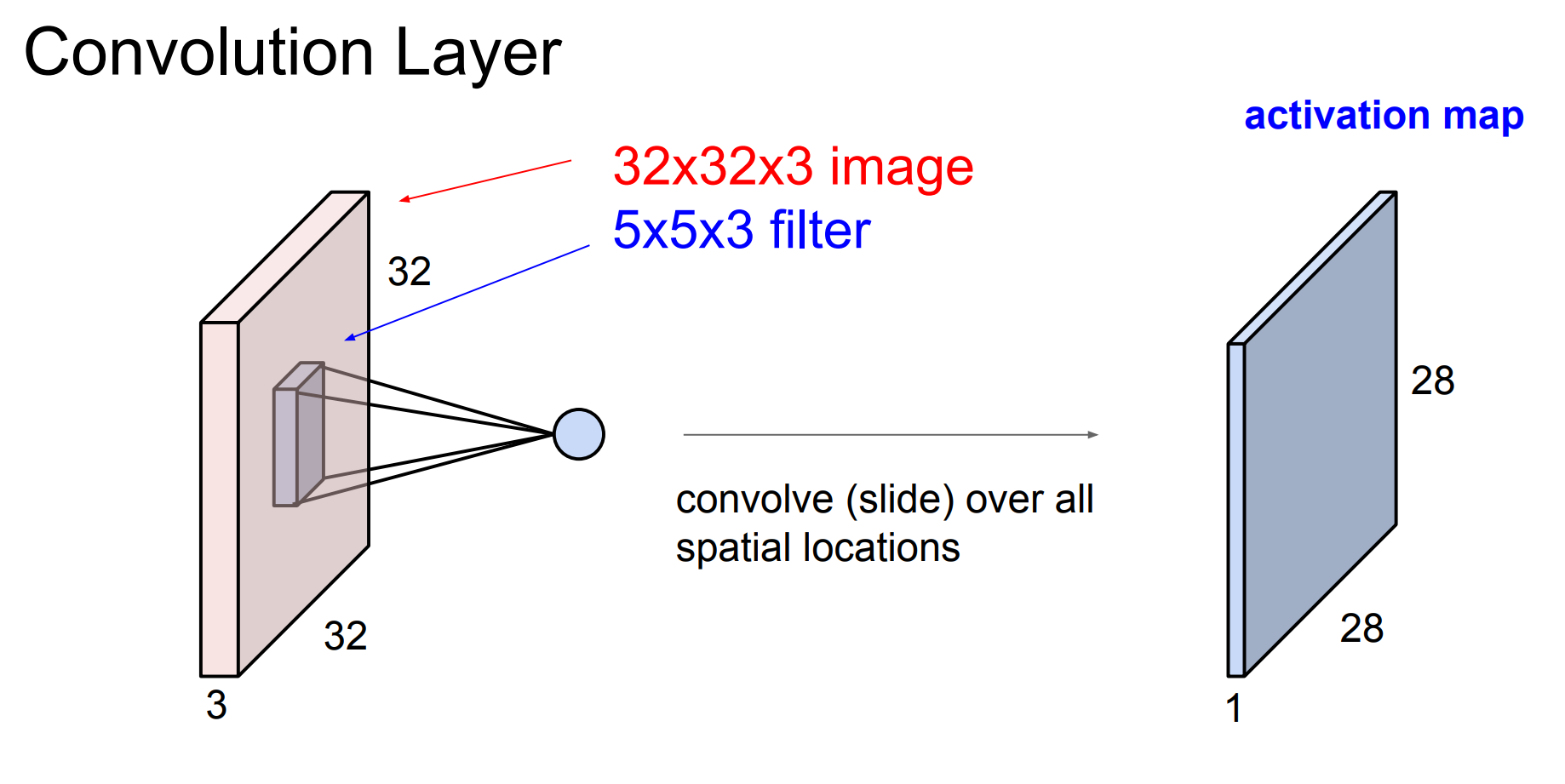
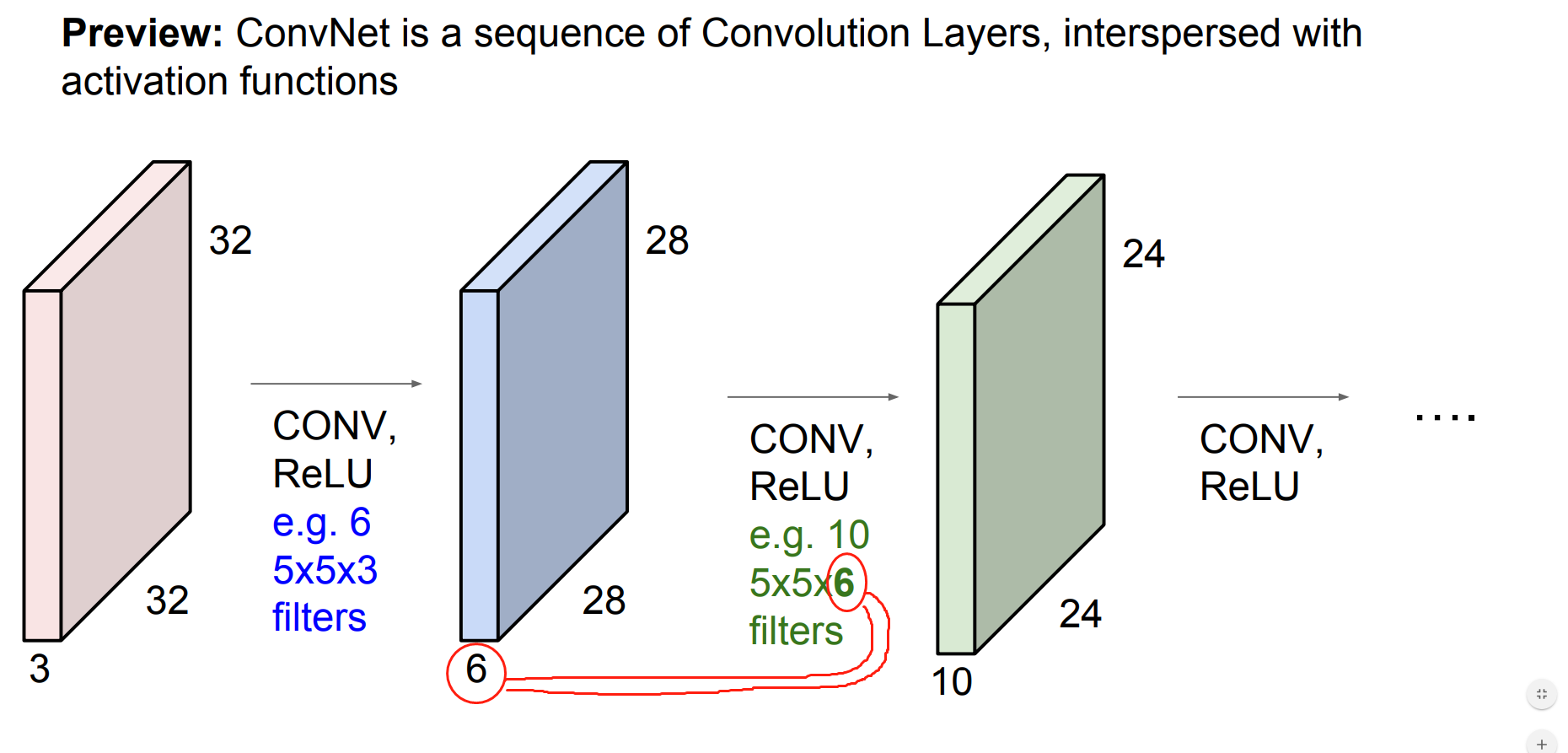
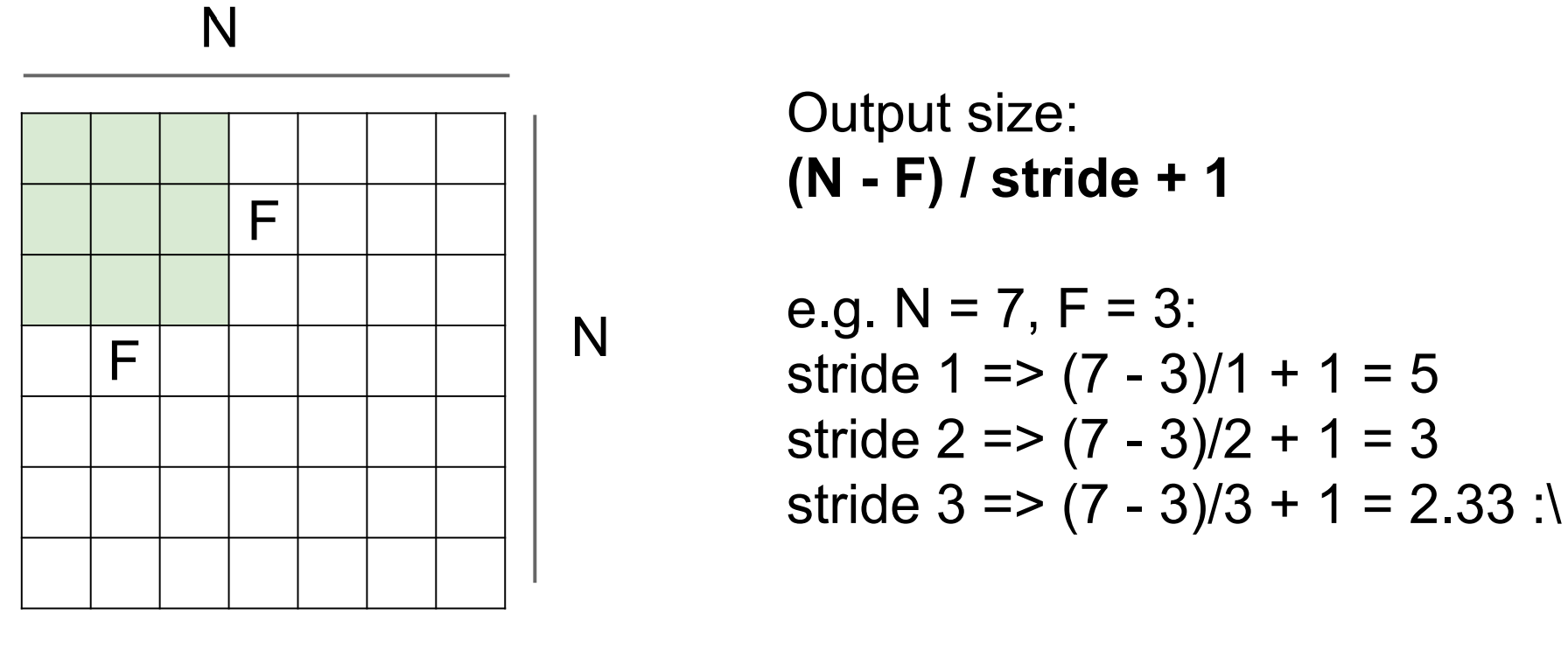
ConvNet notes